C. On What Interval(S) Is F Decreasing and Concave Up. Use to Justify Your Answer
4. Applications of Derivatives
four.5 Derivatives and the Shape of a Graph
Learning Objectives
- Explain how the sign of the first derivative affects the shape of a office'southward graph.
- State the first derivative exam for critical points.
- Employ concavity and inflection points to explicate how the sign of the second derivative affects the shape of a function'south graph.
- Explain the concavity test for a function over an open interval.
- Explain the relationship between a function and its outset and 2nd derivatives.
- State the second derivative test for local extrema.
Earlier in this chapter we stated that if a part ![]() has a local extremum at a point
has a local extremum at a point ![]() then
then ![]() must be a critical point of
must be a critical point of ![]() All the same, a function is not guaranteed to have a local extremum at a critical indicate. For example,
All the same, a function is not guaranteed to have a local extremum at a critical indicate. For example, ![]() has a critical signal at
has a critical signal at ![]() since
since ![]() is cipher at
is cipher at ![]() but
but ![]() does not take a local extremum at
does not take a local extremum at ![]() Using the results from the previous section, nosotros are at present able to determine whether a critical point of a function actually corresponds to a local extreme value. In this section, we also see how the second derivative provides information about the shape of a graph by describing whether the graph of a function curves up or curves downward.
Using the results from the previous section, nosotros are at present able to determine whether a critical point of a function actually corresponds to a local extreme value. In this section, we also see how the second derivative provides information about the shape of a graph by describing whether the graph of a function curves up or curves downward.
The Outset Derivative Test
Corollary iii of the Hateful Value Theorem showed that if the derivative of a function is positive over an interval ![]() then the office is increasing over
then the office is increasing over ![]() On the other hand, if the derivative of the function is negative over an interval
On the other hand, if the derivative of the function is negative over an interval ![]() so the function is decreasing over
so the function is decreasing over ![]() as shown in the post-obit effigy.
as shown in the post-obit effigy.

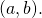 At each indicate
At each indicate 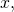 the derivative
the derivative 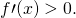 Both functions are decreasing over the interval
Both functions are decreasing over the interval 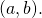 At each indicate
At each indicate  the derivative
the derivative 
A continuous function ![]() has a local maximum at point
has a local maximum at point ![]() if and but if
if and but if ![]() switches from increasing to decreasing at bespeak
switches from increasing to decreasing at bespeak ![]() Similarly,
Similarly, ![]() has a local minimum at
has a local minimum at ![]() if and but if
if and but if ![]() switches from decreasing to increasing at
switches from decreasing to increasing at ![]() If
If ![]() is a continuous office over an interval
is a continuous office over an interval ![]() containing
containing ![]() and differentiable over
and differentiable over ![]() except possibly at
except possibly at ![]() the only way
the only way ![]() can switch from increasing to decreasing (or vice versa) at point
can switch from increasing to decreasing (or vice versa) at point ![]() is if
is if ![]() changes sign every bit
changes sign every bit ![]() increases through
increases through ![]() If
If ![]() is differentiable at
is differentiable at ![]() the just way that
the just way that ![]() can change sign as
can change sign as ![]() increases through
increases through ![]() is if
is if ![]() Therefore, for a role
Therefore, for a role ![]() that is continuous over an interval
that is continuous over an interval ![]() containing
containing ![]() and differentiable over
and differentiable over ![]() except possibly at
except possibly at ![]() the only style
the only style ![]() can switch from increasing to decreasing (or vice versa) is if
can switch from increasing to decreasing (or vice versa) is if ![]() or
or ![]() is undefined. Consequently, to locate local extrema for a function
is undefined. Consequently, to locate local extrema for a function ![]() nosotros await for points
nosotros await for points ![]() in the domain of
in the domain of ![]() such that
such that ![]() or
or ![]() is undefined. Recall that such points are called disquisitional points of
is undefined. Recall that such points are called disquisitional points of ![]()
Annotation that ![]() need non have a local extrema at a critical point. The critical points are candidates for local extrema only. In (Figure), nosotros show that if a continuous function
need non have a local extrema at a critical point. The critical points are candidates for local extrema only. In (Figure), nosotros show that if a continuous function ![]() has a local extremum, information technology must occur at a critical point, just a part may not have a local extremum at a critical point. We show that if
has a local extremum, information technology must occur at a critical point, just a part may not have a local extremum at a critical point. We show that if ![]() has a local extremum at a disquisitional indicate, then the sign of
has a local extremum at a disquisitional indicate, then the sign of ![]() switches as
switches as ![]() increases through that point.
increases through that point.
Using (Figure), we summarize the main results regarding local extrema.
This event is known as the first derivative exam.
We tin can summarize the first derivative examination as a strategy for locating local extrema.
Now let'south look at how to apply this strategy to locate all local extrema for particular functions.
Using the First Derivative Exam to Find Local Extrema
Use the first derivative test to notice the location of all local extrema for ![]() Apply a graphing utility to confirm your results.
Apply a graphing utility to confirm your results.
Employ the first derivative test to locate all local extrema for ![]()
Solution
![]() has a local minimum at -2 and a local maximum at three.
has a local minimum at -2 and a local maximum at three.
Using the Starting time Derivative Exam
Use the first derivative test to find the location of all local extrema for ![]() Use a graphing utility to confirm your results.
Use a graphing utility to confirm your results.
Use the first derivative test to discover all local extrema for ![]()
Concavity and Points of Inflection
We now know how to determine where a office is increasing or decreasing. However, there is another result to consider regarding the shape of the graph of a office. If the graph curves, does it bend upward or bend downward? This notion is chosen the concavity of the role.
(Figure)(a) shows a role ![]() with a graph that curves up. As
with a graph that curves up. As ![]() increases, the slope of the tangent line increases. Thus, since the derivative increases every bit
increases, the slope of the tangent line increases. Thus, since the derivative increases every bit ![]() increases,
increases, ![]() is an increasing function. We say this part
is an increasing function. We say this part ![]() is concave upward. (Figure)(b) shows a function
is concave upward. (Figure)(b) shows a function ![]() that curves downward. Every bit
that curves downward. Every bit ![]() increases, the slope of the tangent line decreases. Since the derivative decreases as
increases, the slope of the tangent line decreases. Since the derivative decreases as ![]() increases,
increases, ![]() is a decreasing office. We say this office
is a decreasing office. We say this office ![]() is concave down.
is concave down.
In general, without having the graph of a office ![]() how tin can nosotros decide its concavity? By definition, a function
how tin can nosotros decide its concavity? By definition, a function ![]() is concave up if
is concave up if ![]() is increasing. From Corollary 3, we know that if
is increasing. From Corollary 3, we know that if ![]() is a differentiable function, then
is a differentiable function, then ![]() is increasing if its derivative
is increasing if its derivative ![]() Therefore, a part
Therefore, a part ![]() that is twice differentiable is concave upwards when
that is twice differentiable is concave upwards when ![]() Similarly, a function
Similarly, a function ![]() is concave down if
is concave down if ![]() is decreasing. We know that a differentiable part
is decreasing. We know that a differentiable part ![]() is decreasing if its derivative
is decreasing if its derivative ![]() Therefore, a twice-differentiable office
Therefore, a twice-differentiable office ![]() is concave downward when
is concave downward when ![]() Applying this logic is known as the concavity exam.
Applying this logic is known as the concavity exam.
We conclude that we can decide the concavity of a function ![]() past looking at the second derivative of
past looking at the second derivative of ![]() In addition, we observe that a function
In addition, we observe that a function ![]() can switch concavity ((Effigy)). Still, a continuous function tin switch concavity only at a bespeak
can switch concavity ((Effigy)). Still, a continuous function tin switch concavity only at a bespeak ![]() if
if ![]() or
or ![]() is undefined. Consequently, to determine the intervals where a function
is undefined. Consequently, to determine the intervals where a function ![]() is concave up and concave downwards, nosotros wait for those values of
is concave up and concave downwards, nosotros wait for those values of ![]() where
where ![]() or
or ![]() is undefined. When we take determined these points, we split up the domain of
is undefined. When we take determined these points, we split up the domain of ![]() into smaller intervals and make up one's mind the sign of
into smaller intervals and make up one's mind the sign of ![]() over each of these smaller intervals. If
over each of these smaller intervals. If ![]() changes sign as we laissez passer through a signal
changes sign as we laissez passer through a signal ![]() then
then ![]() changes concavity. It is important to remember that a function
changes concavity. It is important to remember that a function ![]() may not change concavity at a signal
may not change concavity at a signal ![]() even if
even if ![]() or
or ![]() is undefined. If, however,
is undefined. If, however, ![]() does alter concavity at a bespeak
does alter concavity at a bespeak ![]() and
and ![]() is continuous at
is continuous at ![]() nosotros say the betoken
nosotros say the betoken ![]() is an inflection bespeak of
is an inflection bespeak of ![]()
Testing for Concavity
We now summarize, in (Figure), the information that the first and 2nd derivatives of a role ![]() provide about the graph of
provide about the graph of ![]() and illustrate this data in (Figure).
and illustrate this data in (Figure).
| Sign of | Sign of | Is | Concavity |
|---|---|---|---|
| Positive | Positive | Increasing | Concave upward |
| Positive | Negative | Increasing | Concave downwards |
| Negative | Positive | Decreasing | Concave up |
| Negative | Negative | Decreasing | Concave down |
The 2nd Derivative Exam
The showtime derivative test provides an analytical tool for finding local extrema, but the second derivative can besides be used to locate farthermost values. Using the second derivative tin can sometimes be a simpler method than using the outset derivative.
We know that if a continuous function has a local extrema, it must occur at a critical betoken. However, a part need non have a local extrema at a critical bespeak. Here nosotros examine how the 2nd derivative test can be used to determine whether a function has a local extremum at a disquisitional signal. Let ![]() be a twice-differentiable function such that
be a twice-differentiable function such that ![]() and
and ![]() is continuous over an open interval
is continuous over an open interval ![]() containing
containing ![]() Suppose
Suppose ![]() Since
Since ![]() is continuous over
is continuous over ![]()
![]() for all
for all ![]() ((Figure)). Then, by Corollary 3,
((Figure)). Then, by Corollary 3, ![]() is a decreasing function over
is a decreasing function over ![]() Since
Since ![]() we conclude that for all
we conclude that for all ![]() if
if ![]() and
and ![]() if
if ![]() Therefore, past the offset derivative test,
Therefore, past the offset derivative test, ![]() has a local maximum at
has a local maximum at ![]() On the other hand, suppose in that location exists a signal
On the other hand, suppose in that location exists a signal ![]() such that
such that ![]() just
just ![]() Since
Since ![]() is continuous over an open interval
is continuous over an open interval ![]() containing
containing ![]() so
so ![]() for all
for all ![]() ((Figure)). Then, by Corollary
((Figure)). Then, by Corollary ![]() is an increasing role over
is an increasing role over ![]() Since
Since ![]() we conclude that for all
we conclude that for all ![]()
![]() if
if ![]() and
and ![]() if
if ![]() Therefore, by the kickoff derivative test,
Therefore, by the kickoff derivative test, ![]() has a local minimum at
has a local minimum at ![]()
Note that for case iii. when ![]() and so
and so ![]() may accept a local maximum, local minimum, or neither at
may accept a local maximum, local minimum, or neither at ![]() For example, the functions
For example, the functions ![]()
![]() and
and ![]() all have critical points at
all have critical points at ![]() In each case, the second derivative is zero at
In each case, the second derivative is zero at ![]() Withal, the function
Withal, the function ![]() has a local minimum at
has a local minimum at ![]() whereas the function
whereas the function ![]() has a local maximum at
has a local maximum at ![]() and the function
and the function ![]() does not have a local extremum at
does not have a local extremum at ![]()
Let'due south at present await at how to employ the second derivative test to decide whether ![]() has a local maximum or local minimum at a critical signal
has a local maximum or local minimum at a critical signal ![]() where
where ![]()
Using the 2nd Derivative Exam
Use the second derivative to discover the location of all local extrema for ![]()
We have now adult the tools we demand to determine where a function is increasing and decreasing, as well as acquired an agreement of the basic shape of the graph. In the next section we discuss what happens to a function every bit ![]() At that point, we have enough tools to provide accurate graphs of a large diverseness of functions.
At that point, we have enough tools to provide accurate graphs of a large diverseness of functions.
Primal Concepts
ii. For the function ![]() is
is ![]() both an inflection bespeak and a local maximum/minimum?
both an inflection bespeak and a local maximum/minimum?
Solution
It is not a local maximum/minimum because ![]() does not modify sign
does not modify sign
3. For the function ![]() is
is ![]() an inflection point?
an inflection point?
4. Is it possible for a indicate ![]() to be both an inflection point and a local extrema of a twice differentiable office?
to be both an inflection point and a local extrema of a twice differentiable office?
5. Why do you need continuity for the first derivative examination? Come with an case.
6. Explain whether a concave-downwards function has to cross ![]() for some value of
for some value of ![]()
Solution
False; for case, ![]()
seven. Explain whether a polynomial of degree 2 tin accept an inflection point.
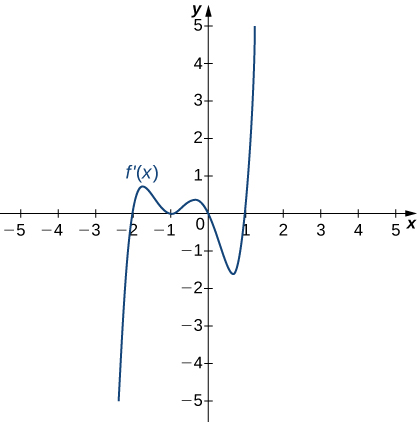
For the following exercises, clarify the graphs of ![]() then list all intervals where
then list all intervals where ![]() is increasing or decreasing.
is increasing or decreasing.
viii.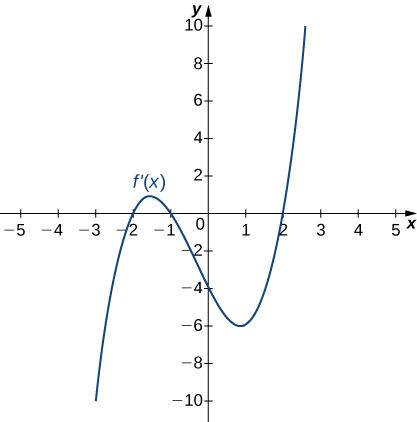
9. 
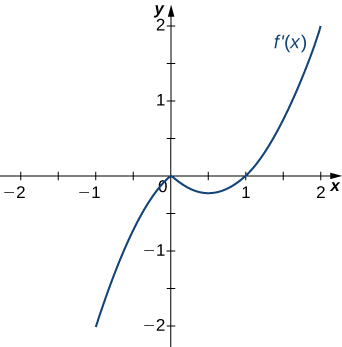
10. 
Solution
Decreasing for ![]() increasing for
increasing for ![]()
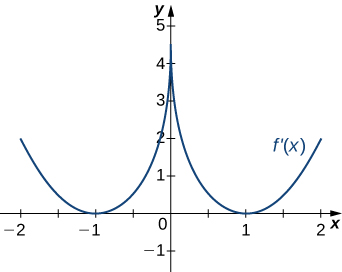
11.
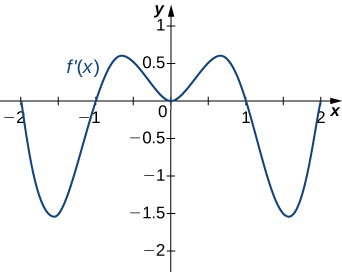
12.
For the following exercises, clarify the graphs of ![]() and so list all intervals where
and so list all intervals where
-
 is increasing and decreasing and
is increasing and decreasing and - the minima and maxima are located.
thirteen.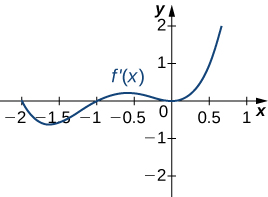
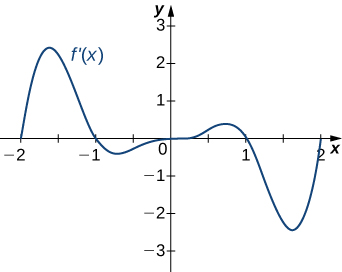
14.
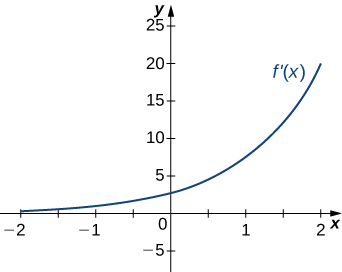
15.
sixteen.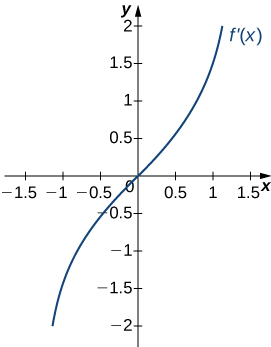
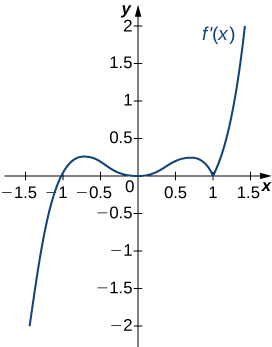
17.
For the following exercises, analyze the graphs of ![]() and so list all inflection points and intervals
and so list all inflection points and intervals ![]() that are concave up and concave downwardly.
that are concave up and concave downwardly.
18.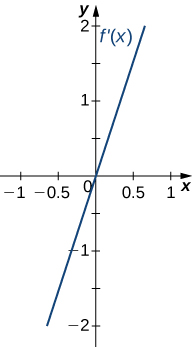
Solution
Concave up on all ![]() no inflection points
no inflection points
nineteen.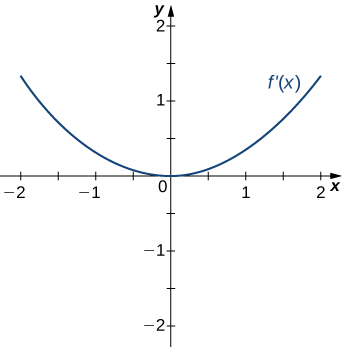
20.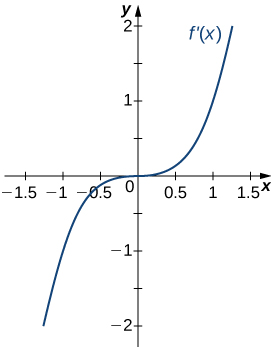
Solution
Concave upward on all ![]() no inflection points
no inflection points
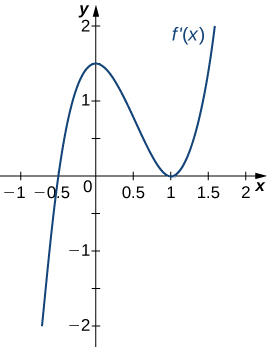
21.
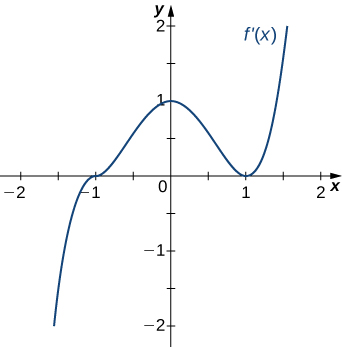
22.
For the following exercises, draw a graph that satisfies the given specifications for the domain ![]() The function does non have to exist continuous or differentiable.
The function does non have to exist continuous or differentiable.
24. ![]() over
over ![]() over
over ![]() for all
for all ![]()
Solution
Answers will vary
26. There is a local maximum at ![]() local minimum at
local minimum at ![]() and the graph is neither concave upwards nor concave down.
and the graph is neither concave upwards nor concave down.
Solution
Answers will vary
For the following exercises, determine
- intervals where
 is increasing or decreasing and
is increasing or decreasing and - local minima and maxima of
28. ![]() over
over ![]()
29. ![]()
For the post-obit exercises, decide a. intervals where ![]() is concave upwards or concave down, and b. the inflection points of
is concave upwards or concave down, and b. the inflection points of ![]()
thirty. ![]()
For the following exercises, make up one's mind
- intervals where
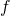 is increasing or decreasing,
is increasing or decreasing, - local minima and maxima of
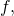
- intervals where
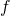 is concave upwards and concave downwardly, and
is concave upwards and concave downwardly, and - the inflection points of
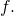
31. ![]()
32. ![]()
33. ![]()
34. ![]()
35. ![]()
36. ![]()
37. ![]()
For the following exercises, make up one's mind
- intervals where
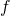 is increasing or decreasing,
is increasing or decreasing, - local minima and maxima of
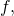
- intervals where
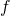 is concave upwards and concave downward, and
is concave upwards and concave downward, and - the inflection points of
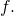 Sketch the bend, then use a calculator to compare your answer. If you cannot decide the exact answer analytically, employ a calculator.
Sketch the bend, then use a calculator to compare your answer. If you cannot decide the exact answer analytically, employ a calculator.
38. [T] ![]() over
over ![]()
39. [T] ![]() over
over ![]()
xl. [T] ![]() over
over ![]()
41. [T] ![]()
42. [T] ![]()
44. ![]() over
over ![]()
45. ![]()
46. ![]()
47. ![]()
For the post-obit exercises, interpret the sentences in terms of ![]()
48. The population is growing more slowly. Here ![]() is the population.
is the population.
Solution
![]()
49. A bike accelerates faster, but a motorcar goes faster. Here ![]() Cycle'due south position minus Car's position.
Cycle'due south position minus Car's position.
50. The airplane lands smoothly. Here ![]() is the plane'due south altitude.
is the plane'due south altitude.
Solution
![]()
51. Stock prices are at their peak. Hither ![]() is the stock price.
is the stock price.
52. The economy is picking up speed. Here ![]() is a measure of the economic system, such as GDP.
is a measure of the economic system, such as GDP.
Solution
![]()
For the following exercises, consider a 3rd-caste polynomial ![]() which has the properties
which has the properties ![]() Determine whether the following statements are truthful or imitation. Justify your answer.
Determine whether the following statements are truthful or imitation. Justify your answer.
53. ![]() for some
for some ![]()
54. ![]() for some
for some ![]()
Solution
True, by the Mean Value Theorem
55. There is no absolute maximum at ![]()
56. If ![]() has 3 roots, so it has one inflection signal.
has 3 roots, so it has one inflection signal.
Solution
True, examine derivative
57. If ![]() has one inflection indicate, so information technology has three real roots.
has one inflection indicate, so information technology has three real roots.
Source: https://opentextbc.ca/calculusv1openstax/chapter/derivatives-and-the-shape-of-a-graph/
0 Response to "C. On What Interval(S) Is F Decreasing and Concave Up. Use to Justify Your Answer"
Post a Comment